【CameraPoseRefinement】以BARF为例介绍三维重建中的位姿优化

@TOC

---

Introduction

在计算机视觉三维重建中，求解3D场景的表示和定位给定的相机帧的相机位姿是两个非常重要的任务，这两个问题互为依赖，一方面，恢复3D场景的表示需要使用已知的相机位姿进行观察；另一方面，定位相机需要来自特征点的可靠对应。

错误的相机位姿会对重建的输出和性能产生一系列负面影响，包括：

1. 图像合成质量下降：

   • 当相机位姿不准确时，生成的视角合成图像可能会出现明显的畸变或模糊，导致最终图像的质量较差。

2. 三维场景表示不准确：

   • 错误的位姿会导致三维场景中的几何结构和深度信息的错误重建，使得模型无法正确理解场景的空间布局。

3. 影像重叠和视差问题：

   • 不准确的位姿可能会造成图像重叠区域的视差不一致，进而导致合成图像中的物体位置、大小等出现明显的不自然或错位现象。

4. 优化过程的困难：

   • 由于相机位姿的误差，优化算法（如Adam）可能会在优化过程中陷入局部最优解，无法收敛到正确的场景表示和相机位置。

5. 训练效率降低：

   • 不准确的相机位姿会使得训练过程变得更加复杂，模型需要更多的迭代才能调整出合理的场景表示，从而延长训练时间。

6. 潜在的视觉伪影：

   • 由于误差，合成图像可能出现视觉伪影（artifacts），如不连贯的阴影、错误的光照等，使得生成的图像看起来不真实。

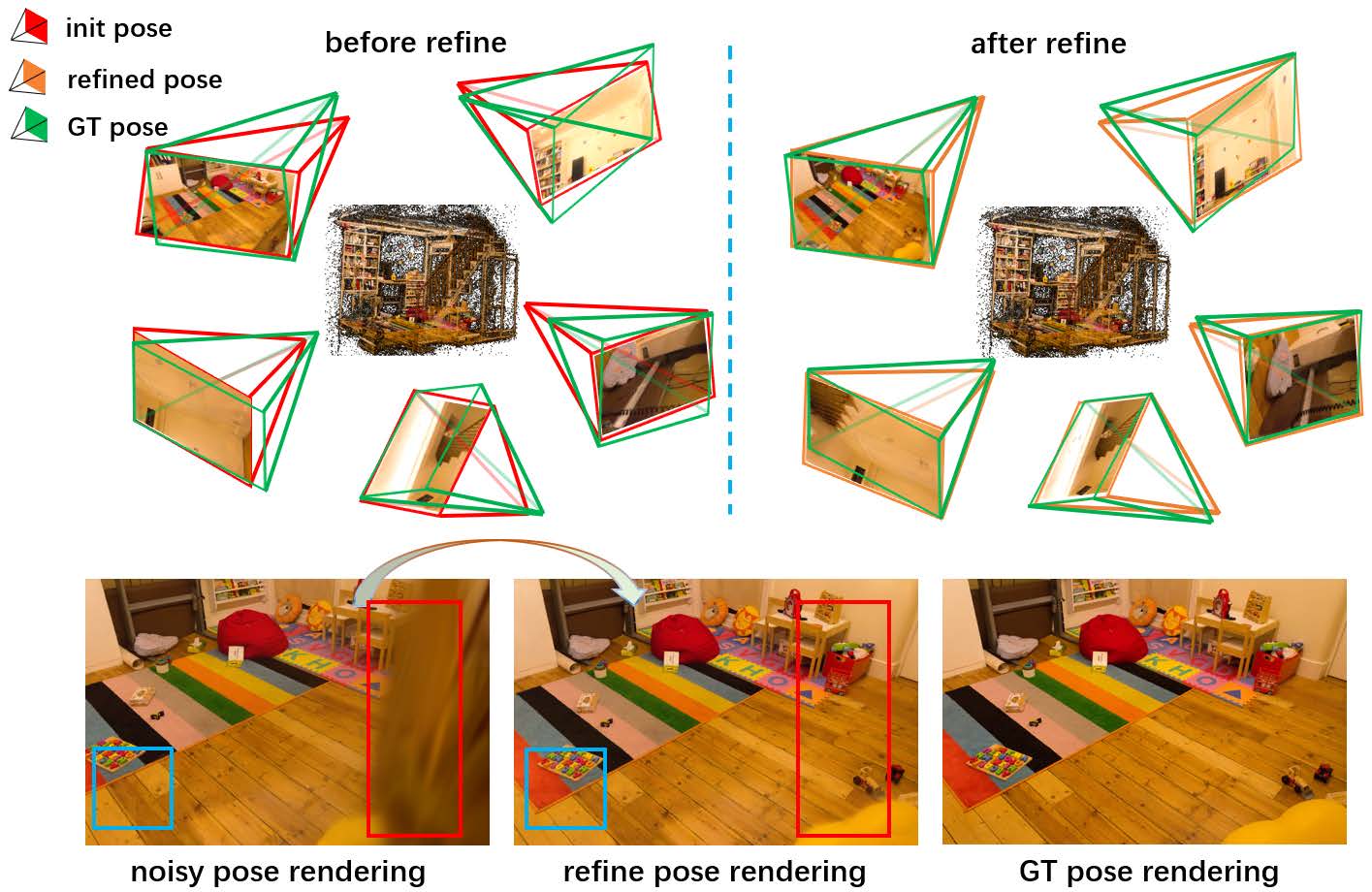
红框是伪影，蓝框是错位。

在《3D Gaussian Splatting for Real-Time Radiance Field Rendering》发布后，很多重建方法都尝试在3D表征上进行创新，它们普遍使用预输入的相机位姿进行重建，而不同时考虑相机位姿的校准，这些预输入的相机位姿通常是由colmap软件估计得到的。此次介绍的两篇文章《BARF》和《HGSLoc》在进行场景重建的同时进行相机位姿的优化，它们使用一些来自不同视角的图像和这些图像的粗略位姿作为输入，并且在相机位姿优化的方法上做出了改进。

Approach

Planar Image Alignment(2D)

首先，BARF考虑2D的平面图像对齐问题。

$$\begin{array}{c} 设\mathbf{x} \in \mathbb{R}^2为像素坐标系下的一个坐标， \\ \mathcal{W}: \mathbb{R}^2 \rightarrow \mathbb{R}^2 是与相机参数\mathbf{p}有关的几何变换，\\ \mathcal{I}: \mathbb{R}^2 \rightarrow \mathbb{R}^3是我们的图像生成过程（图像的3个通道，所以是\mathbb{R}^2 \rightarrow \mathbb{R}^3）， \end{array}$$

我们的目标是使得生成的图片与原图片尽可能地相似，这个联合优化的目标用最小二乘来表达，就是：

$$\min _{\mathbf{p}} \sum_{\mathbf{x}}\left\|\mathcal{I}_{1}(\mathcal{W}(\mathbf{x} ; \mathbf{p}))-\mathcal{I}_{2}(\mathbf{x})\right\|_{2}^{2} .$$

相机参数的维度可以记作

$$\mathbf{p} \in \mathbb{R}^P.$$

这个最小二乘问题的基础迭代步骤可以记作：

$$\Delta \mathbf{p}=-\mathbf{A}(\mathbf{x} ; \mathbf{p}) \sum_{\mathbf{x}} \mathbf{J}(\mathbf{x} ; \mathbf{p})^{\top}\left( \mathcal{I}_{1}(\mathcal{W}(\mathbf{x} ; \mathbf{p})) - \mathcal{I}_{2}(\mathbf{x}) \right).$$

其中，

$$\begin{array}{c} \mathbf{J}是从输出到待优化变量求导的雅克比矩阵，\mathcal{I}_2是给定的ground truth，\\ \mathcal{I}_1是我们想要优化的。而\mathbf{A}(\mathbf{x} ; \mathbf{p})取决于我们选择的优化策略。 \end{array}$$

$$\mathbf{J}(\mathbf{x};\mathbf{p})=\frac{\partial\mathcal{I}_1(\mathcal{W}(\mathbf{x};\mathbf{p}))}{\partial\mathcal{W}(\mathbf{x};\mathbf{p})}\frac{\partial\mathcal{W}(\mathbf{x};\mathbf{p})}{\partial\mathbf{p}}.$$

残差：

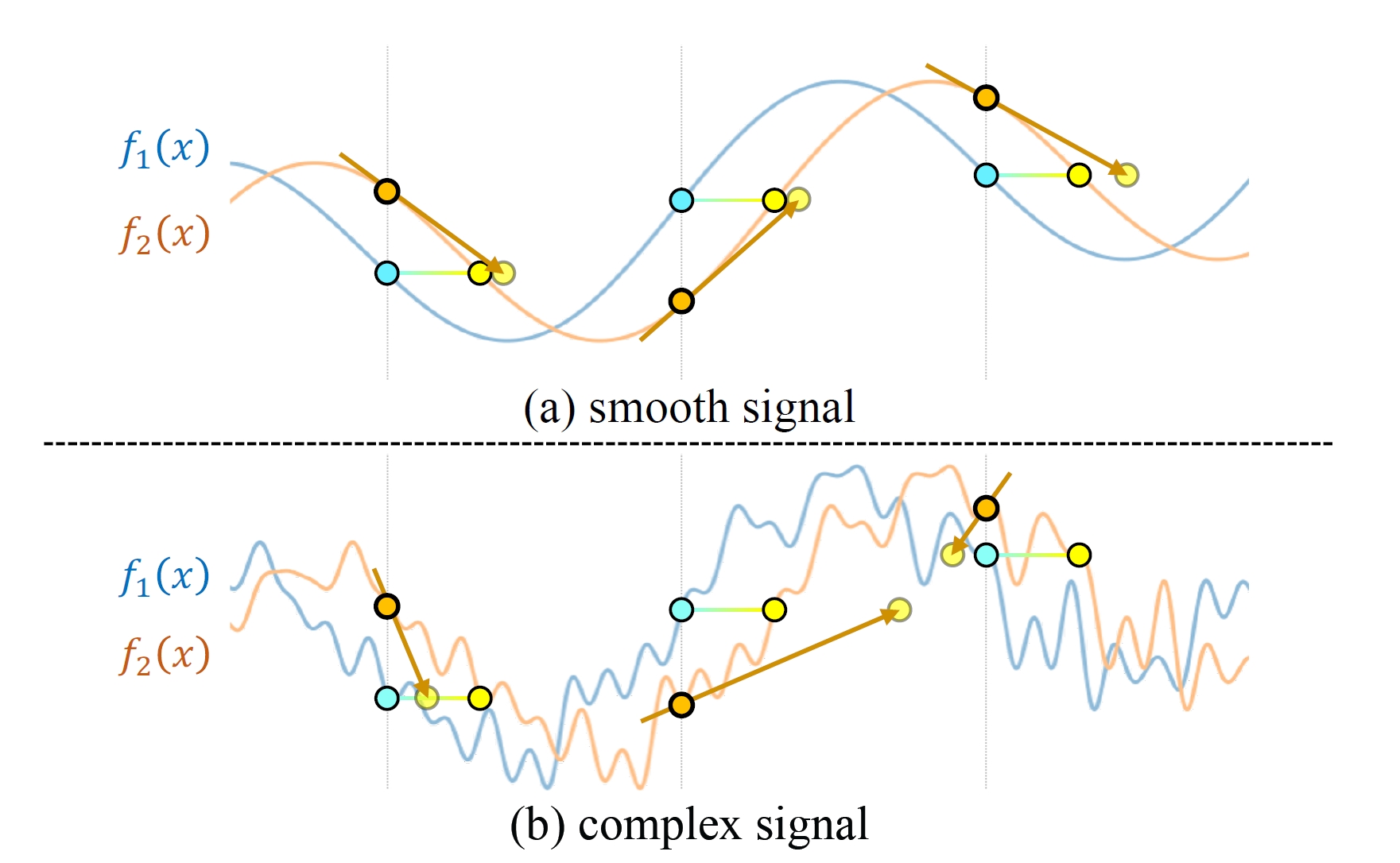
$$\begin{array}{c} \mathbf{r}(\mathbf{x})=\mathcal{I}_{2}(\mathbf{x}) - \mathcal{I}_{1}(\mathcal{W}(\mathbf{x} ; \mathbf{p})).\\ 有的资料中把\mathbf{J}看作是残差对待优化变量的导数，即，\frac{\partial\mathbf{r}}{\partial\mathbf{p}}，\\ 因此，\Delta \mathbf{p}也可以写成： \end{array}$$

$$\Delta \mathbf{p}=-\mathbf{A}(\mathbf{x} ; \mathbf{p}) \sum_{\mathbf{x}} \mathbf{J}(\mathbf{x} ; \mathbf{p})^{\top} \mathbf{r}(\mathbf{x}).$$

$$\begin{array}{c} 如果选择一阶优化方法，\mathbf{A}就是一个标量，也就是学习率；\\ 如果选择二阶优化方法，有时\mathbf{A}(\mathbf{x};\mathbf{p})=(\sum_\mathbf{x}\mathbf{J}(\mathbf{x};\mathbf{p})^\top\mathbf{J}(\mathbf{x};\mathbf{p}))^{-1}，\\ 这取决于具体的优化策略。 \end{array}$$

以上是对这个最小二乘问题的概述。这种基于梯度的优化策略的核心在于输入信号是否足够平滑，否则，很容易陷入局部次优解。输入信号的平滑程度等价于：

$$\frac{\partial\mathcal{I}(\mathbf{x})}{\partial\mathbf{x}}，亦即图像梯度。$$

为了避免局部最优，通常在优化的前期对图像进行模糊处理。图像梯度通过数值差分方法得出，而并非解析的。

$$\begin{array}{c} BARF并没有采用模糊操作，它用神经网络作为\mathcal{I}，优化目标就可以写成：\\ \min_{\mathbf{p}_i,\boldsymbol{\Theta}}\sum_{i=1}^M\sum_\mathbf{x}\left\|f(\mathcal{W}(\mathbf{x};\mathbf{p}_i);\boldsymbol{\Theta})-\mathcal{I}_i(\mathbf{x})\right\|_2^2\\ 其中，f:\mathbb{R}^2 \rightarrow \mathbb{R}^3，\boldsymbol{\Theta}是网络的参数，M是图像个数。\\ 然后，图像梯度就变为可解析的\frac{\partial{f}(\mathbf{x})}{\partial\mathbf{x}}，而不是数值差分的估计。 \end{array}$$

通过操纵网络f，还可以对对齐的信号平滑度进行更原则性的控制，而不必依赖于图像的启发式模糊，从而使这些形式可推广到3D场景表示。稍后，将会介绍barf如何操作f对信号进行平滑度控制。

Neural Radiance Fields (3D)

接下来，BARF将以上过程拓展为3D，具体如下：

$$\begin{array}{c} 多层感知机：f:\mathbb{R}^3 \rightarrow \mathbb{R}^4,\\ MLP参数：\boldsymbol{\Theta},\\ 3D点坐标：\mathbf{x} \in \mathbb{R}^3,\\ 3D点坐标对应的颜色：\mathbf{c} \in \mathbb{R}^3,\\ 体素密度：\sigma \in \mathbb{R},\\ 相机位姿变换：\mathcal{W}，其有6个自由度{x,y,z,\phi,\theta,\psi},故\mathbf{p}\in \mathbb{R}^6,\\ 且，[\mathbf{c};\sigma]^{\top}=f(\mathbf{x};\boldsymbol{\Theta}),\\ 像素齐次坐标：\bar{\mathbf{u}}=[\mathbf{u};1]^{\top} \in \mathbb{R}^3,深度：z_i,\\ \mathbf{x}_i=z_i\bar{\mathbf{u}}. \end{array}$$

体渲染表达式：

$$\begin{array}{c} \hat{\mathcal{I}}(\mathbf{u})=\int_{z_{\mathrm{near}}}^{z_{\mathrm{far}}}T(\mathbf{u},z)\sigma(z\bar{\mathbf{u}})\mathbf{c}(z\bar{\mathbf{u}})\mathrm{d}z ,\\ 其中，z_{\mathrm{near}}和z_{\mathrm{far}}是感兴趣的深度上下限，\mathcal{I}仍然是\mathbb{R}^2 \rightarrow \mathbb{R}^3，\\ 表示这个像素坐标对应的RGB数值。\\ T(\mathbf{u},z)=\exp\bigl(-\int_{z_{\mathrm{max}}}^{z}\sigma(z^{\prime}\bar{\mathbf{u}})\mathrm{d}z^{\prime}\bigr). \end{array}$$

T对应3dgs中的透射率。这两个式子和3dgs的体渲染公式也是极为接近的：

$$C_i=\sum_{n\leq N}c_n\cdot\alpha_n\cdot T_n,\text{ where }T_n=\prod_{m<n}(1-\alpha_m),\\ \alpha_n=o_n\cdot\exp(-\sigma_n),\quad\sigma_n=\frac12\Delta_n^\top\Sigma^{\prime{-1}}\Delta_n.$$

区别在于，3dgs中的T是通过累乘得出，体素密度则取决于椭球投影到平面的形状再乘以不透明度。而nerf中的颜色值和体素密度是通过MLP直接得出。

$$\begin{array}{c} 令\mathbf{y}=[\mathbf{c};\sigma]^{\top}=f(\mathbf{x};\boldsymbol{\Theta}).\\ 继续改写：\hat{\mathcal{I}}(\mathbf{u})=g\left(\mathbf{y}_1,\ldots,\mathbf{y}_N\right),g:\mathbb{R}^{4N} \rightarrow \mathbb{R}^3.\\ \hat{\mathcal{I}}(\mathbf{u};\mathbf{p})=g\Big(f(\mathcal{W}(z_1\bar{\mathbf{u}};\mathbf{p});\boldsymbol{\Theta}),\ldots,f(\mathcal{W}(z_N\bar{\mathbf{u}};\mathbf{p});\boldsymbol{\Theta})\Big),\mathcal{W}:\mathbb{R}^{3} \rightarrow \mathbb{R}^3 . \end{array}$$

最后，这个联合优化问题变为：

$$\min_{\mathbf{p}_1,...,\mathbf{p}_M,\boldsymbol{\Theta}}\sum_{i=1}^M\sum_\mathbf{u}\left\|\hat{\mathcal{I}}(\mathbf{u};\mathbf{p}_i,\boldsymbol{\Theta})-\mathcal{I}_i(\mathbf{u})\right\|_2^2 .$$

Bundle-Adjusting Neural Radiance Fields

barf与Nerf差异最大的一点在于，barf需要在优化网络参数的同时考虑到相机参数。而barf认为直接使用nerf的位置编码方案使得相机参数优化变得困难，对此，barf做出了改进，提出了捆绑优化的动态调整策略，这也是这篇文献最大的贡献之一。

Nerf最初的位置编码方案为：

$$\gamma(\mathbf{x})=\begin{bmatrix}\mathbf{x},\gamma_0(\mathbf{x}),\gamma_1(\mathbf{x}),\ldots,\gamma_{L-1}(\mathbf{x})\end{bmatrix}\in\mathbb{R}^{3+6L} .$$

这里的L是超参数。

$$\gamma_k(\mathbf{x})=\begin{bmatrix}\cos(2^k\pi\mathbf{x}),\sin(2^k\pi\mathbf{x})\end{bmatrix}\in\mathbb{R}^6 .$$

那么，k阶位置编码的雅克比矩阵为：

$$\frac{\partial\gamma_k(\mathbf{x})}{\partial\mathbf{x}}=2^k\pi\cdot\left[-\sin(2^k\pi\mathbf{x}),\cos(2^k\pi\mathbf{x})\right] .$$

它将来自MLP的梯度信号放大，并且其方向以相同频率变化。这使得预测有效更新Δp变得困难，因为来自采样的3D点的梯度信号在方向和幅度方面是不相干的，并且很容易相互抵消。因此，对于barf的联合优化来说，不能直接应用位置编码。

---

barf的做法是从低频段到高频段逐步激活位置编码：

$$\begin{array}{c} \gamma_k(\mathbf{x};\alpha)=w_k(\alpha)\cdot\left[\cos(2^k\pi\mathbf{x}),\sin(2^k\pi\mathbf{x})\right], \\ w_k(\alpha)= \begin{cases} 0 &\text{if }\alpha<k \\ \frac{1-\cos((\alpha-k)\pi)}{2} &\text{if }0\leq\alpha-k<1 \\ 1 &\text{if }\alpha-k\geq1& \end{cases} .\\ \frac{\partial\gamma_k(\mathbf{x};\alpha)}{\partial\mathbf{x}}=w_k(\alpha)\cdot2^k\pi\cdot\left[-\sin(2^k\pi\mathbf{x}),\cos(2^k\pi\mathbf{x})\right]. \\ \alpha \in [o,L] 是与优化进度成正比的可控的一个超参数。 \end{array}$$

从原始3D输入x(α=0)开始，barf逐渐激活较高频段的编码，直到启用完整位置编码(α=L)，相当于原始 NeRF 模型。这使得 BARF 能够通过最初平滑的信号发现正确的Δp，然后将重点转移到学习高保真场景表示。

Experiment

平面图像对齐的定性实验

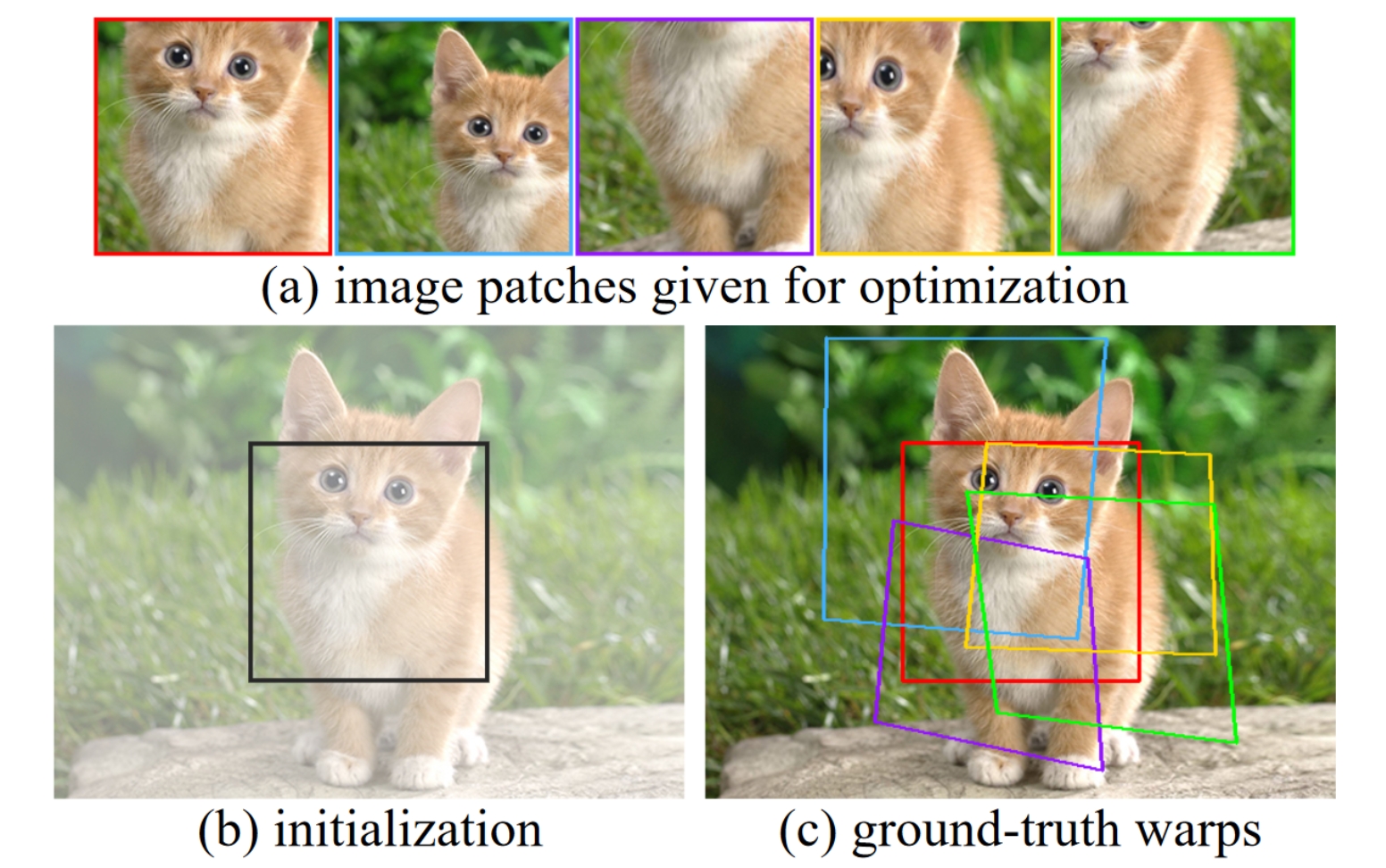
给定图像块，barf的目标是恢复整个图像的对齐和神经网络重建，其中初始化为（b）中所示的中心裁剪，而相应的真实变换（ground-truth warps）如（c）所示。

实验结果：(a)为直接使用位置编码，(b)为不使用位置编码，(c)是barf的结果。

合成场景上的定量实验

Scene	Camera pose registration	View synthesis quality
Rotation (°) ↓	Translation ↓	PSNR ↑	SSIM ↑	LPIPS ↓
full pos.enc.	w/o pos.enc.	BARF	full pos.enc.	w/o pos.enc.	BARF	full pos.enc.	w/o pos.enc.	BARF	ref. NeRF	full pos.enc.	w/o pos.enc.	BARF	ref. NeRF	full pos.enc.	w/o pos.enc.	BARF	ref. NeRF
Chair	7.186	0.110	0.096	16.638	0.555	0.428	19.02	30.22	31.16	31.91	0.804	0.942	0.954	0.961	0.223	0.065	0.044	0.036
Drums	3.208	0.057	0.043	7.322	0.255	0.225	20.83	23.56	23.91	23.96	0.840	0.893	0.900	0.902	0.166	0.116	0.099	0.095
Ficus	9.368	0.095	0.085	10.135	0.430	0.474	19.75	25.58	26.26	26.58	0.836	0.926	0.934	0.941	0.182	0.070	0.058	0.051
Hotdog	3.290	0.225	0.248	6.344	1.122	1.308	28.15	34.00	34.54	34.91	0.923	0.967	0.970	0.973	0.083	0.040	0.032	0.029
Lego	3.252	0.108	0.082	4.841	0.391	0.291	24.23	26.35	28.33	29.28	0.876	0.880	0.927	0.942	0.102	0.112	0.050	0.037
Materials	6.971	0.845	0.844	15.188	2.678	2.692	16.51	26.86	27.48	28.06	0.747	0.926	0.936	0.942	0.294	0.068	0.058	0.049
Mic	10.554	0.081	0.075	22.724	0.356	0.301	15.10	30.93	31.18	31.83	0.788	0.966	0.969	0.971	0.334	0.056	0.049	0.046
Ship	5.506	0.095	0.074	7.232	0.354	0.326	22.12	26.78	27.50	28.00	0.755	0.833	0.849	0.858	0.255	0.175	0.132	0.118
Mean	6.167<	0.202<	0.193	11.303	0.768	0.756	22.12	26.78	27.50	29.40	0.821	0.917	0.930	0.936	0.205	0.087	0.065	0.057