Diffusion & Gaussian Splatting
@TOC
DreamFusion: Text-to-3D using 2D Diffusion (SIGGRAPH 2023)
输入 (Input):
一段描述目标物体的自然语言文本提示 (Text Prompt),例如 "a corgi taking a selfie"。
输出 (Output):
一个完整的 3D场景表示,具体形式为一个神经辐射场 (NeRF) 模型。这个模型可以从任意新视角渲染出高质量的2D图像。
解决的任务 (Task):
零样本文本到3D合成 (Zero-shot Text-to-3D Synthesis)。
核心任务是在完全不使用任何3D训练数据的情况下,仅根据文本输入生成一个连贯、合理的3D模型。
DreamFusion通过开创性的分数蒸馏采样 (Score Distillation Sampling, SDS) 方法,巧妙地利用一个预训练好的2D文本到图像扩散模型作为“知识先验”,来指导和优化一个从零开始的3D NeRF模型,从而将强大的2D生成能力“提升”到3D领域。
Motivation
在DreamFusion出现之前,通过AI生成内容的研究主要集中在2D图像领域。得益于像LAION这样的大规模图文配对数据集,文本到图像(Text-to-Image)模型(如DALL-E 2, Imagen, Stable Diffusion)取得了惊人的成果,能够生成高质量、高分辨率且富有创意的图像。
然而,将这种成功复制到3D领域面临一个核心的巨大挑战:缺乏大规模、高质量的3D数据集。创建带有精确文本标注的3D模型数据集,其成本和难度远超于收集2D图片。现有的3D数据集规模小、多样性差,不足以训练出像2D领域那样强大的生成模型。
DreamFusion的核心动机就是绕过对3D训练数据的依赖。作者们提出了一个革命性的想法:我们能否利用已经训练好的、强大的2D文本到图像扩散模型作为一种“先验知识”或“评判者”,来指导和优化一个3D模型的生成?
这个想法的本质是,一个好的3D模型,当它从任意角度被渲染成2D图像时,这张图像都应该看起来是“合理”的,并且与给定的文本描述相符。而强大的2D生成模型恰好知道什么样的2D图像是“合理”且“与文本相符”的。因此,DreamFusion的目标就是通过优化一个3D表示(具体来说是NeRF),使其在任意视角下的2D渲染结果都能“欺骗”这个2D模型,让2D模型认为这是一个高质量的、符合文本描述的图像。
Architecture
DreamFusion的架构可以理解为一个“生成器-评判者”的优化循环,但这里的“评判者”并非像GAN中的判别器那样需要训练,而是一个预训练好且完全冻结的2D文本到图像扩散模型(论文中使用了Google的Imagen模型)。
整个流程可以分解为以下几个关键部分(参考论文图3):

3D场景表示: 神经辐射场 (NeRF)
DreamFusion不使用传统的网格(Mesh)或体素(Voxel)来表示3D对象,而是采用神经辐射场 (Neural Radiance Field, NeRF)。
NeRF本质上是一个多层感知机(MLP),它的输入是一个3D空间坐标
(x, y, z),输出是该点的体积密度 (Volumetric Density, τ) 和颜色 (Albedo, ρ)。体积密度
τ决定了该点有多“实”,或者说光线穿过它时会被吸收多少。颜色ρ代表了该点材质的基础颜色。在每次生成任务开始时,这个NeRF网络的权重都是随机初始化的。整个优化的目标就是调整这些权重。
可微分渲染器 (Differentiable Renderer)
为了从NeRF得到一张2D图像,需要一个渲染过程。这个过程必须是可微分的,因为我们需要将2D图像上的损失梯度传导回3D NeRF模型的参数上。
渲染过程如下:
在一个随机的机位(camera position)放置一个虚拟相机。
从相机出发,沿着每个像素的方向发射一条光线。
在这条光线上采样一系列3D点,将这些点的坐标输入NeRF,得到它们各自的密度
τ和颜色ρ。通过体积渲染(Volume Rendering)的数学公式,将这些点的信息沿着光线积分,最终计算出该像素的颜色。
为了更好地定义几何形状,论文还加入了着色 (Shading) 步骤。它通过计算密度场的梯度来获得表面法线,并模拟一个随机位置的光源进行光照计算,从而产生明暗效果。
2D先验模型 (The Frozen Critic): 预训练的扩散模型 (Imagen)
这是整个系统的“知识来源”。当NeRF渲染出一张2D图像后,这张图像会被送入一个冻结的(frozen) 2D文本到图像扩散模型。
扩散模型的作用不是生成图像,而是评估渲染出的图像有多么符合给定的文本提示。这是通过一种名为Score Distillation Sampling (SDS) 的新颖损失函数来实现的。
优化循环 (Optimization Loop)
整个过程是一个迭代优化的循环:
第1步: 随机选择一个相机视角和光源。
第2步: 使用可微分渲染器,从当前NeRF模型渲染出一张2D图像。
第3步: 将这张渲染图和目标文本输入SDS损失函数,计算出一个损失值。这个损失值反映了“渲染图在多大程度上不像一个由文本描述的真实图像”。
第4步: 计算损失相对于NeRF网络参数的梯度。
第5步: 使用这个梯度来更新NeRF网络的权重。
这个循环会重复数千次,每次都从不同的随机视角进行渲染和优化。最终,NeRF的参数会收敛,形成一个从各个角度看都符合文本描述的连贯的3D模型。
Method
1. Score Distillation Sampling (SDS) - 核心损失函数
这是DreamFusion最关键的理论贡献。它解决了一个核心问题:如何利用一个扩散模型来优化一个生成器(在这里是NeRF)的参数,而不需要进行成本高昂的反向传播(backpropagation)穿过整个扩散模型的去噪网络(U-Net)。
背景:扩散模型 扩散模型通过两个过程工作:一个“前向”过程,不断给图像加噪声直至其变为纯高斯噪声;一个“反向”过程,学习一个神经网络(通常是U-Net)来逐步去除噪声,从一个随机噪声复原出清晰图像。在文本到图像模型中,这个去噪过程会受到文本提示的引导。
为什么不能直接用扩散模型的训练损失? 一个直观的想法是,把NeRF渲染出的图像
x当作一张“真实图像”,然后用扩散模型的原始训练损失来优化x。扩散模型的损失大致是这样的:其中
x_t是加噪后的图像,y是文本,ε是加入的真实噪声,ε_φ是模型预测的噪声。如果直接最小化这个损失来优化x(进而优化NeRF的参数θ),梯度会非常复杂,因为它包含一个U-Net的雅可比矩阵项∂ε_φ/∂x_t。这一项计算成本极高,且在噪声水平较低时非常不稳定,导致优化失败。SDS的巧妙之处 SDS提出了一种新的梯度计算方式,它避免了对扩散模型U-Net的求导。其梯度形式如下:
我们可以直观地理解这个梯度:
ε_φ(x_t; y) - ε: 这一项是噪声的残差。ε_φ是扩散模型预测的噪声,ε是我们实际加入的噪声。这个差值可以看作是一个“更新方向”。如果预测的噪声和真实噪声很接近,说明渲染图x已经很好了,更新就小。如果差很远,说明x需要被修改。最重要的是,ε_φ被视为一个固定的预测结果,梯度不会流经它,即stop_gradient(ε_φ)。∂x/∂θ: 这一项是渲染器相对于NeRF参数的雅可比矩阵。它将图像空间的更新方向(ε_φ - ε)转换回参数空间的梯度。整体效果: SDS的损失函数在每次迭代时,都用扩散模型来预测一个“理想的”去噪方向,然后将这个方向作为监督信号,通过可微分渲染器更新NeRF的参数。这就像一个老师(扩散模型)在不断地给学生(NeRF)指出错误,但老师本身是固定的,不会被学生影响。

2. 3D模型与渲染的细节
为了让SDS更好地工作并生成高质量的3D几何,论文对NeRF的结构和渲染过程做了几项关键的修改和改进。
着色以解耦几何与外观 (Shading for Geometry) 传统的NeRF直接预测与视角相关的颜色(radiance)。这会导致一个问题:模型可能会学会在一个简单的几何形状(比如一个平面)上“画”出复杂的纹理,从特定角度看似乎是3D的,但实际上没有真实的几何结构。 为了解决这个问题,DreamFusion的NeRF不直接输出最终颜色,而是输出与视角无关的材质反照率(albedo, ρ)。最终的像素颜色是通过以下方式计算的:
通过计算体积密度
τ场相对于空间坐标μ的负梯度,来得到该点的表面法线向量n = -∇_μ τ。将这个法线
n、材质颜色ρ、以及随机采样的光源l结合,使用一个简单的漫反射光照模型(Lambertian reflection)来计算最终的着色颜色c。 这个设计至关重要,因为它强迫模型学习一个有意义的密度场。如果密度场是平的或混乱的,计算出的法线就会是错误的,着色效果就会很差,从而得到很高的SDS损失。只有当密度场形成了平滑、连贯的表面时,着色效果才会好。
无纹理渲染 (Textureless Rendering) 为了进一步强化几何的学习,在训练过程中,模型会以一定概率(例如50%)忽略NeRF预测的颜色
ρ,而是直接使用纯白色进行着色渲染。在这种情况下,渲染出的图像只包含光照和阴影信息,完全没有纹理。这迫使优化过程必须生成一个正确的3D几何形状来匹配文本描述(例如,“一个松鼠”的轮廓和明暗关系),而不是仅仅在平面上画一个松鼠的图片。视角相关的文本提示 (View-Dependent Prompting) 一个简单的文本提示,如“一匹马”,并没有指定视角。当从马的背面渲染时,扩散模型可能会感到困惑,因为它可能更熟悉马的正面或侧面图像。这会导致所谓的“Janus问题”(双面神问题),即模型在物体的背面也生成一个正面。 DreamFusion通过在提示中加入视角信息来解决这个问题。根据随机采样的相机方位角,它会自动在原始提示后面追加“front view”、“side view”或“back view”等文本。这为扩散模型在每个视角下都提供了一个明确的、无歧义的指导,极大地提升了最终3D模型的一致性和质量。
几何正则化器 (Geometry Regularizers) 论文还使用了一些额外的损失项来规范几何形状,防止出现不希望的“悬浮物”或空洞,并鼓励法线方向朝向相机,这有助于稳定训练过程。
总结来说,DreamFusion的成功在于其巧妙地将两个不同领域的强大技术结合起来:它利用神经辐射场(NeRF) 作为灵活的、可微分的3D表示,并开创性地提出了分数蒸馏采样(SDS),将一个预训练的2D扩散模型转化为一个强大的3D对象“梦想家”(Dreamer),在没有任何3D数据的监督下,仅凭文本描述就能“凭空”创造出丰富多样的3D世界。
Text-to-3D using Gaussian Splatting (CVPR 2024)
输入 (Input):
一段描述所需3D物体的文本提示 (Text Prompt),例如“一只毛茸茸的柯基的高质量照片”。
输出 (Output):
一个高质量、细节丰富的3D模型,其具体表示形式为3D高斯溅射 (3D Gaussian Splatting)。
解决的任务 (Task):
文本到3D内容的生成 (Text-to-3D Generation)。该任务旨在根据自然语言描述自动创建一个三维数字资产。
这篇论文着重解决了以往方法中的两大痛点:1)通过引入额外的3D点云先验来直接指导几何生成,从而显著缓解了导致模型前后不分的 “雅努斯问题” (Janus Problem);2)利用3D高斯溅射的显式特性和新的致密化策略,生成了具有毛发、羽毛等 高频细节 的精细模型。
Motivation
在GSGEN这篇论文出现之前,主流的文本到3D (Text-to-3D)生成技术,特别是那些基于分数蒸馏采样 (Score Distillation Sampling, SDS) 的方法,普遍面临两大核心挑战:
几何形状不准确和“雅努斯问题”(Janus Problem):许多先前的方法,如DreamFusion,使用像神经辐射场 (NeRF) 这样的隐式3D表示方法。 NeRF将场景几何和外观编码在一个神经网络的权重中,这是一种“黑箱”操作。这种隐式特性使得直接引入或编辑3D几何先验(priors)变得非常困难。其结果是,模型在优化过程中完全依赖于从不同视角渲染的2D图像与预训练的2D扩散模型进行比较(即SDS损失)。这种纯2D的监督信号很容易导致几何上的不一致,最典型的表现就是“雅努斯问题”(Janus Problem),即生成的3D模型从任何角度看都像一个“正面”,例如一个前后都有脸的人头。
生成耗时长且细节不足:基于NeRF的优化过程通常非常耗时,因为它需要在每次迭代中进行大量的光线追踪和神经网络前向传播。 此外,这些方法在生成具有高频细节(如毛发、羽毛、精细纹理)的3D模型时也常常力不从心,最终结果的表面往往过于平滑。
因此,这篇论文的核心动机就是解决上述问题,即生成几何精确、细节丰富且3D一致性强的高质量3D模型。作者认为,要实现这一目标,关键在于选择一种新的3D表示方法,它必须是显式的 (explicit),从而能够轻松地整合3D几何先验来直接指导和约束模型的形状生成。他们最终选择了当时最新的、最先进的显式表示方法——3D高斯溅射 (3D Gaussian Splatting)。
Architecture
GSGEN模型的核心架构是一个两阶段的渐进式优化策略,旨在平衡几何结构的准确性和纹理细节的丰富性。整个流程如下图所示:

GSGEN的整体流程可以概括为:
初始化 (Initialization):根据输入的文本提示词,使用一个预训练的文本到点云模型 (Point-E) 生成一个粗糙的、符合文本描述的初始点云。 这个点云被用作初始3D高斯球的位置。
第一阶段:几何优化 (Geometry Optimization):此阶段的目标是塑造出一个几何合理、3D一致的粗略形状。它同时受到两种监督信号的联合指导:
2D 图像扩散先验:通过传统的SDS损失,确保从任意视角渲染出的图像符合文本描述。
3D 点云扩散先验:这是本文的关键创新之一。通过一个额外的3D SDS损失,直接在3D空间中约束高斯球的位置,使其符合一个由点云扩散模型引导的合理形状,从而有效缓解“雅努斯问题”。
第二阶段:外观优化 (Appearance Refinement):在获得了合理的几何基础后,此阶段专注于丰富模型的纹理细节和外观。 在这个阶段,模型只使用2D图像扩散先验 (2D SDS loss) 来优化高斯球的颜色、透明度等属性。 同时,为了增强细节和保真度,作者引入了一种新的、基于紧凑性的高斯球致密化策略 (compactness-based densification)。
这个两阶段的设计哲学非常清晰:先搭好骨架,再画好皮肉。通过解耦几何和外观的优化过程,GSGEN能够更有效地解决各自的挑战。
Method
第一阶段:几何优化 (Geometry Optimization)
这一阶段的目标是解决几何问题,特别是“雅努斯问题”。 作者观察到,一个点云可以被看作是一组各向同性的高斯球。 因此,他们提出直接用一个预训练的文本到点云的扩散模型 (Point-E) 来指导高斯球位置的优化。
他们没有直接将高斯球的位置与Point-E生成的点云进行对齐(因为这会涉及配准、缩放等难题),而是巧妙地设计了一个3D SDS损失。 这样,优化的过程就变成了一个联合优化问题,其损失函数如下:
我们来详细解析这个公式的每个部分:
第一项 (2D SDS Loss):这是标准的SDS损失。
$\theta$ 代表所有3D高斯球的可优化参数。
$x=g(\theta)$ 是通过可微分渲染器从当前3D高斯球渲染出的2D图像。
$x_t$ 是添加了噪声$t$步后的图像。
$\epsilon_\phi(x_t; y, t)$ 是预训练的2D图像扩散模型(如Stable Diffusion)在给定文本$y$的条件下,预测出的噪声。
$\epsilon_I$ 是实际添加的噪声。
这一项的作用是驱动3D模型在渲染后看起来像文本所描述的样子。
第二项 (3D SDS Loss):这是GSGEN的核心创新。
$p$ 代表所有3D高斯球的中心位置集合。
$p_t$ 是添加了噪声$t$步后的点云。
$\epsilon_\psi(p_t; y, t)$ 是预训练的3D点云扩散模型 (Point-E) 在给定文本$y$的条件下,预测出的3D空间中的噪声。
这一项的作用是直接在3D空间中对高斯球的位置进行约束,强迫它们组成一个符合文本描述的、3D一致的形状。
$\lambda_{3D}$ 是一个权重系数,用于平衡2D和3D损失。
通过这种2D和3D先验的联合引导,模型可以在早期就形成一个合理的几何结构,有效避免了坍塌和“雅努斯问题”。

第二阶段:外观优化 (Appearance Refinement)
当有了一个好的几何骨架后,模型进入第二阶段,专注于细节和外观。实验发现,如果在这一阶段继续使用3D先验,反而会干扰外观的学习,导致细节不足。 因此,这一阶段只使用2D SDS损失。
这个公式除了标准的SDS损失外,还包含了正则化项来修剪不必要的高斯球。
此阶段最重要的技术点是基于紧凑性的致密化 (Compactness-based Densification)。
背景:原始的3D高斯溅射论文中,致密化(即增加高斯球的数量)是基于视图空间的位置梯度。如果一个高斯球在屏幕上看起来很大(梯度大),它就会被分裂或复制,以填充细节。
问题:在SDS的随机梯度指导下,这种策略会遇到困境。如果分裂的阈值设得太低,随机的大梯度会导致高斯球数量爆炸式增长;如果阈值设得太高,又无法生成足够的细节,导致表面过于平滑。
GSGEN的方案:作者提出了一种全新的、作为补充的致密化策略。具体来说,对于每个高斯球,模型会找到它在3D空间中的K个最近邻。如果它与某个邻居的距离小于它们半径之和(即它们在空间上发生了重叠或接触),就在它们之间生成一个新的高斯球来“填补空洞”(fill the holes)。
效果:这种方法不依赖于不稳定的梯度,而是根据高斯球在空间中的几何分布来进行致密化,能够生成更连续、更完整的几何表面,从而获得更高的保真度和细节。
初始化策略 (Initialization with Geometry Prior)
如前所述,一个好的开始至关重要。如果从一个简单的模式(如随机球体)开始初始化,模型很容易陷入局部最优,生成对称或退化 (degenerated) 的3D对象。
为了克服这一点,GSGEN采用了一个预训练的文本到点云模型Point-E来生成一个粗糙的几何初始化。 具体步骤是:
输入文本提示,例如 "a DSLR photo of a panda"。
Point-E模型输出一个包含数千个点的3D点云,这个点云在形状上大致符合一只熊猫的轮廓。
GSGEN使用这些点的3D坐标作为初始3D高斯球的中心位置。
高斯球的颜色被随机初始化(实验发现直接使用Point-E生成的颜色效果不佳),而缩放和不透明度则被设置为固定的初始值。
这种初始化方式通过提供一个非对称的、符合语义的几何先验,极大地帮助模型“打破对称性”,从一开始就朝着正确的方向优化,是实现高质量生成的关键一步。
总结
总而言之,GSGEN通过以下几个关键的技术创新,显著提升了Text-to-3D的生成质量:
采用显式的3D高斯溅射表示,为直接整合3D先验提供了可能性。
设计了两阶段优化策略,将复杂的生成任务解耦为“几何优化”和“外观优化”,分而治之。
在几何优化阶段引入3D SDS损失,通过联合2D和3D扩散先验,从根本上缓解了“雅努斯问题”,保证了3D一致性。
在外观优化阶段提出基于紧凑性的致密化策略,解决了原生致密化方法在SDS下的不稳定性,有效提升了模型细节。
使用文本到点云模型进行几何初始化,为优化提供了一个良好的起点,避免了生成退化的结果。
这些设计共同作用,使得GSGEN能够生成比以往方法更快速、几何更准确、细节更丰富的3D资产。
GaussianDreamer: Fast Generation from Text to 3D Gaussians (CVPR 2024)
输入 (Input):
一个描述你想要创建的3D物体的 文本提示 (Text Prompt)。例如,“一个维京战斧,幻想风格,武器” 或 “一只狐狸”。
输出 (Output):
一个高质量、细节丰富的 3D高斯溅射 (3D Gaussian Splatting) 模型。这个模型可以被实时渲染成任意视角的2D图像。
解决的任务 (Task):
快速、高质量的文本到3D模型生成 (Fast Text-to-3D Generation)。
此前的Text-to-3D方法要么速度慢、要么3D结构一致性差、要么细节不足。GaussianDreamer通过一个创新的两阶段方法解决了这个难题:首先用一个快速的3D扩散模型生成一个结构正确的粗糙“骨架”,然后利用一个强大的2D扩散模型为这个骨架快速“绘制”上丰富的几何和外观细节,最终在保证3D一致性的同时,以极快的速度(约15分钟)生成了高质量的3D模型。
Motivation
近年来,从文本直接生成3D模型(Text-to-3D)取得了显著进展,主要分为两大技术路线:
基于3D数据的扩散模型 (3D Diffusion Models):这类模型直接在文本-3D配对数据上进行训练。它们的优点是能够生成具有良好三维一致性的模型(例如,物体不会出现多个正面或结构混乱)。然而,其缺点也非常明显:高质量的3D数据集既昂贵又稀缺,规模远小于2D图像数据集。这导致这类模型泛化能力有限,难以生成训练数据中未见过的新颖、复杂物体,并且生成的细节(如纹理和精细几何)通常比较粗糙。
提升2D扩散模型至3D (Lifting 2D Diffusion Models to 3D):这类方法利用了强大的、在海量图文数据上预训练的2D扩散模型(如Stable Diffusion)。它们通过一种名为分数蒸馏采样(Score Distillation Sampling, SDS)的技术,在不同视角下渲染一个3D表示(如NeRF),并用2D模型指导其优化,使其渲染图符合文本描述。这种方法的优点是泛化能力极强,可以生成非常精细、富有创造力的细节和外观。但其主要缺点是缺乏全局的3D一致性,容易产生“Janus问题”(即物体有多个正面),因为2D模型本身没有三维空间的概念。同时,优化过程通常非常耗时(数小时)。
GaussianDreamer的动机正是为了结合上述两种方法的优点,同时规避它们的缺点。作者的目标是创建一个既能保证3D结构一致性,又能生成丰富细节,并且生成速度极快的Text-to-3D框架。他们发现,最近提出的 3D高斯溅射(3D Gaussian Splatting) 是一种非常高效、显式的3D表示方法,非常适合作为连接这两种扩散模型的桥梁。
因此,论文的核心思想是:
用一个快速的3D扩散模型生成一个粗糙但结构正确的3D“骨架”或先验。
将这个粗糙模型转换为3D高斯表示。
利用强大的2D扩散模型对这个3D高斯表示进行快速优化,为其添加丰富的几何和外观细节。
Architecture
GaussianDreamer的整体框架可以概括为一个两阶段的流程:“3D模型先验初始化” 和 “2D模型优化”。我们可以参考论文中的图2来理解整个过程。

阶段一:使用3D扩散模型先验进行初始化 (Initialization with 3D Diffusion Model Priors)
生成粗糙3D资产:输入一个文本提示(Prompt),例如“a fox”。首先,使用一个预训练的3D扩散模型(如Shap-E或Text-to-Motion模型)快速生成一个基础的3D资产。这个资产通常是网格(Mesh)或点云形式,它定义了物体的基本形状和姿态,保证了3D结构的正确性。
转换为点云:将生成的3D网格转换为点云(Point Clouds)。点云包含了每个点的位置和颜色信息。
点云增强:由于初始生成的点云可能比较稀疏,颜色也比较单调,论文引入了 “噪声点增长 (Noisy Point Growing)” 和 “颜色扰动 (Color Perturbation)” 操作。这一步会增加点云的密度,并丰富其颜色变化,为后续优化提供更好的基础。
初始化3D高斯:使用增强后的点云来初始化一组3D高斯。每个高斯球由位置、颜色、不透明度、协方差(决定形状和旋转)等参数定义。至此,我们得到了一个初始的、由3D高斯表示的物体。这个阶段非常快,大约只需要几秒钟。
阶段二:使用2D扩散模型进行优化 (Optimization with the 2D Diffusion Model)
可微分渲染:在任意虚拟相机视角下,使用3D高斯溅射技术将这组3D高斯渲染成一张2D图像。这个渲染过程是可微分的,意味着我们可以计算出图像像素值相对于每个高斯参数的梯度。
分数蒸馏采样 (SDS) 损失:将渲染出的2D图像和输入的文本提示一起送入一个强大的预训练2D扩散模型(如Stable Diffusion)。2D模型会判断这张图像“有多像”由该文本提示生成的图像,并给出一个“指导”方向(梯度)。这个过程就是通过SDS损失实现的。
参数更新:利用SDS损失计算出的梯度,反向传播来更新3D高斯的参数(位置、颜色、形状等)。
迭代优化:重复步骤1至3,从不同视角渲染并优化。由于初始的3D高斯已经有了很好的几何先验,这个优化过程收敛得非常快,只需大约15分钟,就能将粗糙的3D模型变得细节丰富、纹理逼真。
最终,我们就得到了一个高质量、可通过高斯溅射进行实时渲染的3D模型。
Method
整体框架
如前所述,框架分为两步:
初始化:利用3D扩散模型
F_3D,根据文本y生成一个网格m = F_3D(y)。然后将m转化为增强的点云,并用此点云初始化一组3D高斯θ_b。优化:使用2D扩散模型
F_2D和SDS损失,对初始高斯θ_b进行迭代优化,得到最终的精细化高斯θ_f。
第一阶段:使用3D扩散模型先验进行高斯初始化
这是确保3D一致性和快速收敛的关键。论文讨论了两种类型的3D模型。
使用Text-to-3D扩散模型 (如Shap-E)
生成网格和颜色:使用像Shap-E这样的模型,输入文本后,它会生成一个隐式表示(如符号距离函数SDF),从中可以提取出三角网格
m。同时,模型也会预测出网格顶点的颜色。转换为初始点云:将网格
m的顶点坐标作为点云的位置p_m,顶点颜色作为点云的颜色c_m。这样得到初始点云pt_m = (p_m, c_m)。问题:这个初始点云有两个问题:位置
p_m太稀疏,几何细节不足;颜色c_m通常比较简单平滑。噪声点增长和颜色扰动 (关键步骤):为了解决上述问题,论文设计了以下流程(参考图3和算法1):
计算边界框 (BBox):首先计算初始点云
p_m的最小包围盒。均匀采样新点:在这个边界框内,均匀地随机生成大量新的点,记为
p_r。筛选新点:为了让新生成的点附着在物体表面附近而不是随机散布,需要进行筛选。论文使用了一个高效的数据结构KDTree来加速查找。对于每一个新点
p_uinp_r,在原始点云p_m中找到离它最近的点p_vn。如果它们之间的距离小于一个很小的阈值(例如0.01),就保留这个新点p_u。为新点赋色并扰动:对于被保留下来的新点,它的颜色
c_r被设置为其最近邻点p_vn的颜色c_m[i],并加上一个小的随机扰动a(0到0.2之间)。这增加了颜色的丰富性。合并点云:将原始点云
pt_m和经过筛选和着色的新点云pt_r = (p_r, c_r)合并,得到最终用于初始化的稠密点云pt = (p_f, c_f)。这里的
⊕表示拼接操作。
初始化3D高斯参数:
位置和颜色:将最终点云的位置
p_f和颜色c_f直接作为3D高斯的位置μ_b和颜色c_b。不透明度:所有高斯的不透明度
α_b统一初始化为一个较小的值,如0.1。协方差:高斯的初始形状(由协方差
Σ_b决定)被设置为各向同性(球形),其大小与该点到其最近邻点的距离成正比。这确保了高斯的大小能大致覆盖物体表面。
使用Text-to-Motion扩散模型
这种方法主要用于生成特定姿态的3D虚拟人(avatar)。
生成人体姿态:输入描述动作的文本(如“一个人用左腿踢”),使用Text-to-Motion模型生成一系列人体运动骨架。
选择并转换为SMPL模型:从生成的动作序列中选择一个最符合文本描述的姿态,并将其转换为SMPL(一种参数化的人体模型)网格
m。转换为点云:将SMPL网格的顶点作为点云的位置
p_m。由于SMPL模型通常没有纹理,点云的颜色c_m被随机初始化。归一化:为了将模型移动到坐标原点附近,计算所有点
p_m的中心点p_c,然后将所有点的位置减去该中心点。初始化:使用处理后的点云
pt来初始化3D高斯,过程与3.3.1节中的步骤5完全相同。

第二阶段:使用2D扩散模型进行优化
这个阶段的目标是为已经具备良好3D结构的初始高斯模型添加丰富的细节。
渲染:在每一轮迭代中,从一个随机的相机视角,使用3D高斯溅射渲染器
g来渲染当前的3D高斯θ_i,得到2D图像x = g(θ_i)。计算梯度:应用前面介绍的SDS损失。将渲染图像
x、文本y输入2D扩散模型F_2D,并根据公式(1)计算出用于更新高斯参数的梯度。更新参数:使用计算出的梯度来更新所有3D高斯的参数
θ_i(包括位置、颜色、不透明度、缩放、旋转)。例如,对于颜色参数,更新规则就是color = color - learning_rate * color_gradient。迭代:重复这个“渲染 -> 计算梯度 -> 更新”的过程。论文中提到总共进行1200次迭代。由于有了良好的初始化,优化过程可以集中在学习细节上,而不是从零开始构建3D结构,因此速度非常快。
通过这种方式,GaussianDreamer巧妙地将3D模型的全局结构一致性与2D模型的强大细节生成能力结合在了一起,并通过高效的3D高斯溅射表示实现了极快的生成速度。
DreamGaussian: Generative Gaussian Splatting for Efficient 3D Content Creation (ICLR 2024 oral)
输入 (Input):
(模式一) 一张 单视角图像 (Single-view image) 及其前景蒙版。
(模式二) 一段 文本描述 (Text prompt)。
输出 (Output):
一个高质量、带有UV纹理贴图的 3D三角网格模型 (3D textured mesh),可直接用于下游应用(如游戏、动画)。
解决的任务 (Task):
高效的2D到3D内容生成。该论文旨在解决此前基于优化(如使用NeRF和分数蒸馏采样SDS)的3D生成方法普遍存在的速度极其缓慢的核心痛点。
通过首次将渲染速度极快的 3D高斯溅射 (3D Gaussian Splatting) 应用于生成任务,DreamGaussian 将原先需要数小时的单个3D模型生成过程加速到仅需2分钟,极大地提升了3D内容创作的效率。
Motivation
近年来,利用AI进行3D内容创作取得了显著进展,尤其是在文本到3D(Text-to-3D)和图像到3D(Image-to-3D)领域。现有方法主要分为两大类:
推理式方法 (Inference-only methods):这类方法通常在大型3D数据集上进行预训练,能够快速生成3D模型。然而,它们面临的主要挑战是高质量的3D数据集难以获取,导致生成模型的通用性、多样性和真实感有限。
基于优化的“2D提升”方法 (Optimization-based 2D lifting methods):这类方法,如以DreamFusion为代表的工作,巧妙地利用强大的预训练2D扩散模型(如Stable Diffusion)作为先验知识,通过一种名为分数蒸馏采样 (Score Distillation Sampling, SDS) 的技术来指导3D模型的优化。这种方法不依赖大规模3D数据,通用性更强。
然而,基于优化的方法普遍存在一个核心痛点:优化过程极其缓慢。它们通常采用神经辐射场(Neural Radiance Fields, NeRF)作为3D表示。NeRF需要为每个像素投射光线并沿光线进行密集采样来渲染图像,这个过程计算量巨大,导致单个3D模型的生成通常需要数小时。这种低效率严重限制了其实际应用。
DreamGaussian的核心动机就是要解决这一效率瓶颈,在保持高质量生成效果的同时,大幅提升3D内容的创建速度。作者观察到,NeRF在生成任务中的空间剪枝技术(用于加速)效果不佳,因为SDS提供的梯度是模糊和不一致的,难以判断哪些空间区域是空的。因此,他们寻求一种新的3D表示方法,既能保证渲染质量和效率,又能更好地适应生成式任务的优化过程。
Architecture
DreamGaussian提出了一个两阶段的框架,旨在实现效率与质量的平衡。
第一阶段:生成式高斯溅射 (Generative Gaussian Splatting) 这一阶段的目标是快速生成一个粗略但合理的3D模型。
核心思想: 放弃NeRF,转而采用3D高斯溅射 (3D Gaussian Splatting) 作为3D表示。3D高斯溅射是一种显式的、基于点的表示方法,其中场景由成千上万个三维高斯分布来描述。相比NeRF的隐式表示和体积渲染,它的渲染速度极快,因为它利用了高效的GPU光栅化管线。
输入: 单张图片或一段文本描述。
过程:
初始化: 在一个球形空间内随机初始化一组3D高斯。
生成式优化: 在一个循环中,从随机视角渲染当前3D高斯的图像,并利用2D扩散模型(如Zero-1-to-3用于Image-to-3D,Stable Diffusion用于Text-to-3D)作为先验,通过SDS损失来优化这组3D高斯的所有参数(位置、旋转、缩放、颜色、不透明度)。
渐进式致密化: 在优化过程中,周期性地对高斯进行分裂或克隆,以增加模型的细节,这类似于3D高斯溅射在重建任务中的做法,但频率更高,以适应生成任务从无到有的过程。
输出: 一组经过优化的3D高斯,它们共同构成了一个3D场景的初步表示。这个阶段非常快,通常在1-2分钟内完成。
第二阶段:高效的网格提取和纹理优化 (Efficient Mesh Extraction and Texture Refinement) 直接由3D高斯生成的模型虽然速度快,但通常比较模糊,并且不是下游应用(如游戏、动画)所期望的标准化格式(如三角网格)。因此,第二阶段旨在将高斯表示转换为高质量的纹理网格。
过程:
网格提取 (Mesh Extraction):设计了一种高效的算法,通过查询3D高斯生成的密度场来提取表面几何。具体来说,它通过查询局部高斯密度生成一个密度网格,然后使用经典的移动立方体 (Marching Cubes) 算法来生成三角网格。
纹理烘焙 (Color Back-projection):从多个视角渲染第一阶段生成的3D高斯模型,然后将渲染出的颜色反向投影到提取出的网格表面上,生成一个初始的、但可能较为粗糙的UV纹理贴图。
UV空间纹理优化 (UV-Space Texture Refinement):这是提升最终质量的关键一步。直接在UV空间使用SDS进行优化会导致纹理出现色块和过饱和等问题。作者借鉴了图像编辑方法SDEdit的思想,采用了一种基于均方误差(MSE)的优化策略。具体流程是:
从任意视角渲染当前的纹理网格,得到一张粗糙的图像。
对这张图像添加噪声,然后使用2D扩散模型对其进行多步降噪处理,得到一张更精细、更真实的图像。
将这张“精炼后”的图像作为目标,通过计算它与原始渲染图像之间的MSE损失,来优化UV纹理贴图。
输出: 一个高质量、带有精细纹理贴图的三角网格模型,可以直接用于各种下游应用。这个阶段也非常快,大约50个优化步骤即可完成。
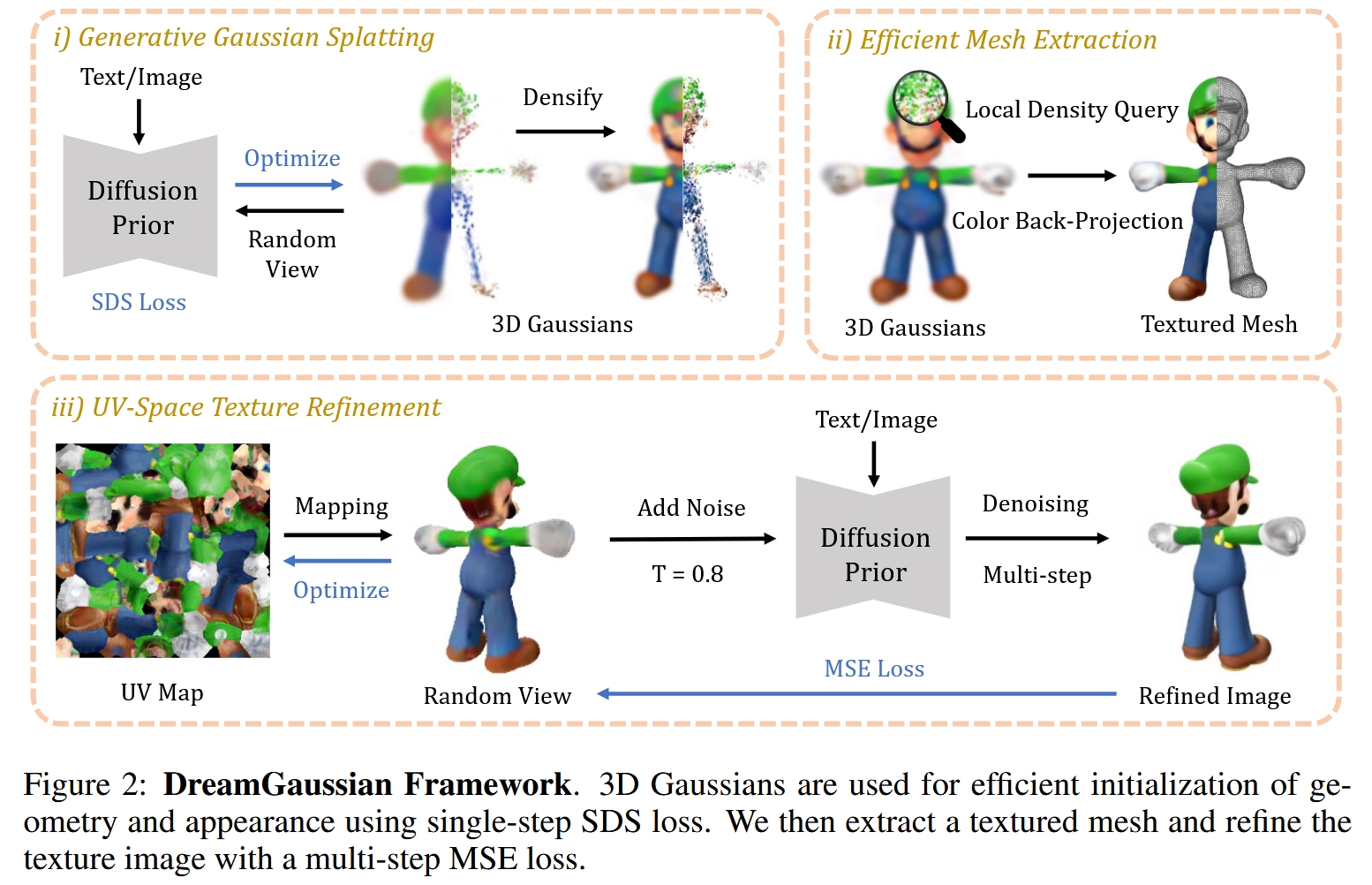
图示:DreamGaussian的两阶段框架。第一阶段使用生成式高斯溅射快速生成3D表示;第二阶段提取网格并进行UV空间纹理优化。
Method
1. 生成式高斯溅射 (Generative Gaussian Splatting)
3D高斯表示: 一个3D高斯由以下参数定义:
位置 (Position)
x:一个三维向量,表示高斯的中心。旋转 (Rotation)
q:一个四元数,表示高斯的旋转方向。缩放 (Scaling)
s:一个三维向量,表示高斯在三个轴向上的大小,共同定义了协方差矩阵。颜色 (Color)
c:一个三维向量,通常是RGB值。不透明度 (Opacity)
α:一个标量,控制高斯的透明度。
与原始的3D高斯溅射论文不同,本文禁用了球谐函数(Spherical Harmonics),因为生成任务中主要关注的是基础的漫反射颜色,而非复杂的视图相关效果。
优化过程:
初始化: 在半径为0.5的球体内随机撒点,生成约5000个初始3D高斯。它们的初始不透明度为0.1,颜色为灰色,缩放为单位大小,没有旋转。
SDS损失 (Score Distillation Sampling Loss):这是优化的核心驱动力。其基本思想是,从任意视角P渲染出的图像
I_RGB,在经过2D扩散模型φ看来,应该是“真实”的。SDS损失的计算如下:首先,将渲染图像
I_RGB加入噪声ε,噪声水平由时间步t控制。然后,让扩散模型预测这个噪声,得到
ε_φ(I_RGB_noisy; t, e),其中e是条件(文本嵌入或图像信息)。损失即为预测噪声与真实噪声之间的差异
w(t)(ε_φ(...) - ε),这个梯度会反向传播,用于更新3D高斯的所有参数Θ。对于Image-to-3D: 使用Zero-1-to-3 XL模型作为扩散先验。它不仅接收文本条件,还能接收参考图像和相对相机位姿
Δp,从而生成新视角的图像。此外,还有一个参考视图损失L_Ref,确保从原始视角渲染出的图像和透明度与输入图像保持一致。这个损失的权重在训练中会线性增加,以确保最终模型能精确匹配输入视图。对于Text-to-3D: 使用Stable Diffusion模型作为先验,条件
e是输入文本的CLIP嵌入。
渐进式致密化 (Progressive Densification):与重建任务不同,生成任务是从一个稀疏的随机状态开始的。因此,DreamGaussian采用了更频繁的致密化策略。
每100个训练步骤(对于Text-to-3D是50步),就会检查高斯的状态。
如果一个高斯累积的梯度过大(表明该区域需要更多细节)并且自身尺寸较小,它就会被克隆 (clone) 一份,并轻微移动位置。
如果一个高斯过大,它会被分裂 (split) 成两个更小的高斯。
同时,不透明度过低(几乎透明)的高斯会被剪枝 (prune) 掉。 这种“先生长,后修剪”的策略非常适合生成任务,能快速地勾勒出物体的形状。

2. 高效的网格提取 (Efficient Mesh Extraction)
直接从数百万个离散的3D高斯中提取网格是一个未被充分探索的问题,暴力计算每个空间点的密度会非常慢。
局部密度查询 (Local Density Query):作者提出了一种分块查询的策略来加速。
首先,将
(-1, 1)的立方体空间划分为16x16x16个重叠的块。对于每个块,只考虑中心点落入该块内的3D高斯。这一步极大地减少了每个查询点需要计算的高斯数量,利用了3D高斯溅射中高斯通常较为局部的特性。
在每个小块内部,再进行
8x8x8的密度查询,最终形成一个128x128x128的全局密度网格。在每个查询点
x,其密度d(x)的计算方式是所有相关高斯i对其贡献的加权和:其中
Σ_i是由缩放s_i和旋转q_i构建的协方差矩阵。
移动立方体与后处理:
得到密度网格后,设定一个经验阈值(例如1.0),使用经典的移动立方体 (Marching Cubes) 算法从密度场中提取出等值面,生成三角网格。
初始网格可能不规则,因此会使用网格重划分 (remeshing) 和抽取 (decimation) 算法(如Cignoni et al., 2008中提出的方法)进行后处理,使其拓扑结构更均匀、更平滑。
3. UV空间纹理优化 (UV-Space Texture Refinement)
颜色反向投影 (Color Back-projection):
首先,使用
xatlas等工具对提取的网格进行UV展开 (UV unwrapping),为每个顶点分配一个二维的UV坐标,并初始化一张空的纹理图。然后,从多个固定的标准视角(例如8个方位角、3个仰角,外加顶部和底部视图)渲染第一阶段生成的3D高斯模型。
对于渲染出的每个图像的每个像素,根据其在网格上的投影位置和UV坐标,将颜色信息“烘焙”到UV纹理图的对应位置上。这个过程类似于将多张照片贴到一个白模上,形成一个初始的纹理。
基于MSE的纹理优化:
问题: 直接用SDS优化UV纹理,由于光栅化渲染器中mipmap技术的存在(为了抗锯齿,会对纹理进行降采样),模糊的SDS梯度会被传播到不同层级的mipmap上,导致最终纹理出现大面积的纯色块和过饱和现象。
解决方案: 借鉴SDEdit的思想,将优化目标从模糊的“分数匹配”转变为明确的“图像匹配”。
生成目标图像: 在每个优化步骤中,从一个随机视角
p渲染当前带纹理的网格,得到一个较为模糊的图像I_coarse。对
I_coarse添加特定强度(由起始时间步t_start控制)的噪声ε。t_start的选择很重要,它决定了噪声的强度,既要足以激发扩散模型生成新的细节,又不能强到完全破坏原始图像的结构和颜色。将这个加噪后的图像输入到2D扩散模型中,进行多步降噪(而不是SDS中的单步预测),得到一张精炼后的图像
I_fine。
MSE损失: 计算
I_fine和I_coarse之间的均方误差 (Mean Squared Error, MSE) 损失。这个损失会通过可微分渲染器反向传播,只更新UV纹理图的像素值。由于
I_fine是明确的像素目标,梯度非常清晰,从而避免了SDS带来的问题,能够生成清晰、细节丰富的纹理。训练细节: 这个阶段只需要大约50个优化步骤,非常快速。对于Image-to-3D任务,仍然会保留参考视图损失,以确保对输入图像的忠实度。
总结
DreamGaussian通过引入3D高斯溅射作为核心3D表示,并设计了一个两阶段的优化框架,成功地解决了现有基于优化的3D生成方法效率低下的核心痛点。
动机清晰: 针对NeRF在生成任务中优化慢的问题,寻找更高效的替代方案。
架构巧妙:
第一阶段利用高斯溅射的快速渲染特性和生成式优化的灵活性,在分钟级别内快速构建3D模型的雏形。
第二阶段通过高效的网格提取和创新的基于MSE的纹理优化策略,将粗糙的高斯表示转换为高质量、可直接用于下游应用的纹理网格,并巧妙地规避了直接使用SDS优化纹理的陷阱。
技术细节扎实: 无论是在生成式高斯溅射的渐进式致密化策略,还是在网格提取的局部密度查询,以及纹理优化的SDEdit思想借鉴上,都体现了作者对问题深入的理解和创新的解决方案。
最终,DreamGaussian在保证生成质量可与主流方法媲美的前提下,实现了约10倍的速度提升,将原先数小时的等待缩短至几分钟,极大地推动了AI 3D内容生成的实用化进程。
GSD: View-Guided Gaussian Splatting Diffusion for 3D Reconstruction (ECCV 2024)
输入 (Input):
一张任意物体的 单视角2D图像 (Single RGB image)。
该图像对应的 相机位姿 (Camera pose)。
输出 (Output):
一个完整的、高质量的 3D高斯溅射 (Gaussian Splatting) 模型。
解决的任务 (Task):
单视图三维重建 (Single-View 3D Reconstruction)。这是一个极具挑战性的任务,因为需要从有限的2D信息中推断出完整的三维几何形状和纹理。
GSD 训练一个扩散模型来学习三维物体(以GS形式表示)的通用“长相”先验。在重建时,它以输入的单张图像作为“向导”,通过一种新颖的可微分渲染引导机制,将一个随机的3D高斯噪声“雕刻”成与输入视图完全匹配的特定3D模型。
Overview
这篇文章提出了一种名为 GSD (Gaussian Splatting Diffusion) 的新方法,用于从单张二维图像重建高质量的三维物体。其核心思想是巧妙地将两种前沿技术结合起来:
高斯溅射 (Gaussian Splatting, GS): 一种新兴、高效且高质量的显式三维表示方法,能够非常逼真地渲染物体。
扩散模型 (Diffusion Model): 一种强大的深度生成模型,擅长学习复杂的数据分布并生成高质量的样本。
GSD 的主要贡献在于,它是首个直接在原始 GS 表示上构建扩散模型的工作。该模型首先在无条件的情况下学习大量三维物体的“通用长相”(即生成先验),然后在重建时,利用输入图像作为“向导”,通过一种新颖的“视图引导采样”策略,将这个通用的三维模型“雕刻”成与输入图像完全一致的特定三维物体。
Motivation
从单张图片重建三维物体是一个极具挑战性的“不适定问题”(ill-posed problem),因为一张二维图片丢失了深度信息,理论上可以对应无数种三维形状。为了解决这个问题,模型需要具备强大的“想象能力”,即拥有关于三维物体应有样貌的先验知识。现有方法主要有以下几类,但都存在明显缺陷:
2D novel view synthesis (新视角合成) 方法: 这类方法本质上是 2D 图像生成模型,虽然能生成不同角度的逼真图像,但由于缺乏真正的 3D 几何约束,生成的多个视角组合在一起时往往会出现三维不一致的问题(比如物体局部结构扭曲、漂移)。
基于显式 3D 表示的方法: 例如使用体素 (Voxel)、点云 (Point Cloud) 或网格 (Mesh) 的方法。这些方法能保证三维几何的一致性,但通常受限于分辨率或拓扑结构的复杂性,导致重建的几何形状较为粗糙,渲染出的图像质量也欠佳。
基于隐式 3D 表示的方法 (如 NeRF): 这类方法将三维场景表示为一个神经网络,能够实现非常逼真的渲染效果。但它们的缺点是几何提取过程(如通过 Marching Cubes)非常繁琐和耗时,并且渲染速度较慢,难以实现实时交互。
GSD 的切入点: 作者们认为,问题的关键在于找到一个“完美”的三维表示方法。高斯溅射 (GS) 恰好弥补了上述方法的不足:
显式几何: 它由一组三维高斯椭球体构成,几何结构是明确的。
高质量渲染: 它的渲染管线是可微分的,并且可以实时渲染出照片级的图像。
灵活性: 相比网格,它没有固定的拓扑约束,更容易由神经网络生成。
因此,本文的动机就是:能否构建一个强大的生成模型,直接学习高斯溅射表示的分布,从而同时拥有强大的三维几何先验和高质量的渲染能力? 扩散模型正是实现这一目标的最佳选择。
Method
GSD 的方法论可以分为三个核心部分:学习 GS 的生成先验、视图引导的采样重建,以及渲染质量的抛光与复用。
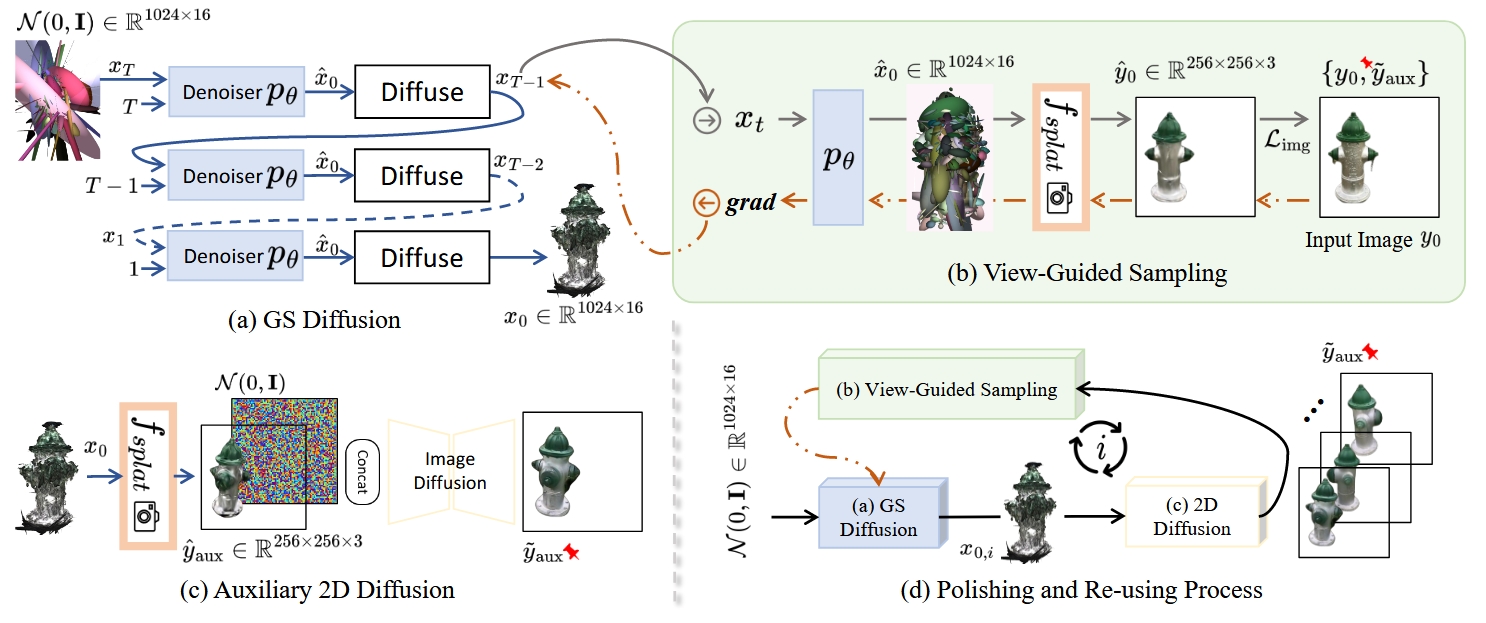
1. 学习高斯溅射的生成先验 (Modeling GS Generative Prior)
这一阶段的目标是训练一个无条件的扩散模型,让它学会生成“看起来合理”的三维物体(以 GS 的形式)。
1. 三维表示 (3D Representation): 首先,需要一个用于训练的数据集。作者将现有的三维物体数据集(如 CO3D)中的每个物体都用官方的 GS 方法预先重建,并进行处理,得到一个 GS 表示的数据集。 为了方便模型学习,每个物体的 GS 表示被规范化为 固定数量 (N=1024) 的高斯椭球体。每一个椭球体由一个 16 维的向量来描述,包含以下信息:
位置 (Position): 3D 空间坐标 (x, y, z),3个维度。
协方差 (Covariance): 决定了椭球体的形状和朝向。它由一个缩放向量 (scale, 3维) 和一个旋转四元数 (rotation, 4维) 共同定义。在模型中,为了稳定,可能直接使用能够表达旋转和缩放的6个独立参数。
颜色 (Color): RGB 颜色值,3个维度。
不透明度 (Opacity): 一个标量,控制该椭球体的透明度,1个维度。
所以,一个三维物体就被表示成一个形状为 (1024, 16) 的张量。
2. 扩散模型 (Diffusion Model): 模型采用标准的 Denoising Diffusion Probabilistic Models (DDPM) 框架。
前向过程 (Forward Process): 在训练时,从数据集中取出一个干净的 GS 物体
x₀,然后通过 T 个步骤逐渐向其添加高斯噪声,得到一系列越来越模糊的噪声版本x₁,x₂, ...,xᴛ。逆向过程 (Reverse Process): 训练一个神经网络
pθ,其任务是在任意一个噪声步t,给定加噪后的样本xᴛ,预测出原始的干净样本x₀(或等价地,预测出所添加的噪声)。其训练目标函数如下:
这个公式的含义是,模型 pθ 的预测值要尽可能地接近真实的、未加噪的 x₀。
3. 骨干网络:Diffusion Transformer (DiT) (Backbone Network): 预测噪声的神经网络 pθ 选择了 Transformer 架构。这是一个关键的技术选择。因为 GS 物体本质上是一组无序的“点”(每个点带有16个特征),Transformer 的自注意力机制非常擅长捕捉这种集合中元素之间的复杂关系。相比于专门为点云设计的网络(如 PVCNN),作者认为 GS 的16个特征维度之间存在很强的内部关联(例如,位置和协方差就紧密相关),Transformer 能够更好地学习这些复杂的特征依赖,从而更好地掌握 GS 数据的分布。 此外,由于 GS 表示本身已经包含了显式的 3D 位置信息,所以这个 Transformer 模型不需要额外的位置编码。
通过以上训练,模型 pθ 就成了一个强大的“三维物体生成器”,只要给它一堆随机高斯噪声,它就能通过 T 步的迭代去噪,生成一个全新的、合理的三维 GS 物体。

2. 视图引导的采样与重建 (View-Guided Sampling)
这是整个方法最核心和巧妙的部分。在训练完成后,我们有了一个能生成随机物体的无条件模型。现在的问题是,如何让它生成一个特定的、与我们提供的输入图像 y₀ 相匹配的物体?
GSD 不采用 在训练时就将图像作为条件的常规做法,而是在推理采样阶段对去噪过程进行“引导”。这个过程在每一个去噪步骤 t 都会执行:
无条件预测: 在第
t步,我们有一个加噪的 GS 样本xᴛ。首先,让已经训练好的无条件扩散模型pθ进行一次标准的预测,得到一个对最终干净物体x₀的初步估计,记为x̂₀。可微分渲染: 将这个预测出的
x̂₀,通过高斯溅射的可微分渲染函数fsplat,从输入图像y₀对应的相机视角进行渲染,得到一张渲染图像ŷ₀。计算引导梯度: 比较渲染图像
ŷ₀和真实的输入图像y₀之间的差异。这个差异通常用一个损失函数来衡量,例如 L1 或 L2 损失,记为L_img。因为整个渲染过程是可微分的,我们可以计算这个损失
L_img相对于当前噪声样本xᴛ的梯度∇xᴛ(L_img)。这个梯度就是一个“修正信号”,它指明了xᴛ应该朝哪个方向微调,才能让它最终生成的物体的渲染结果更接近输入图像y₀。执行引导: 将这个计算出的梯度,以一定的权重
λ_gd(guidance scale),“注入”到当前的去噪步骤中,从而对采样过程进行修正。简单来说,就是用这个梯度来“推”一下当前的xᴛ,让它走向一个更好的方向。修正后的去噪公式大致如下:这里的
StandardDenoiseStep表示标准的 DDPM/DDIM 采样步骤。
通过在每一步都重复这个“预测-渲染-求梯度-引导”的循环,随机初始化的噪声就会被逐步引导,最终收敛成一个与输入视图高度一致的三维 GS 物体。

3. 抛光与复用:提升渲染质量 (Polishing and Re-using)
作者发现,仅通过上述流程重建的 GS,其渲染图有时会出现一些微小的、针状的视觉瑕疵。这是因为从单一视图重建时,模型对于纹理的推断可能不完美。为了解决这个问题,他们引入了一个辅助的 2D 扩散模型,并设计了一个迭代优化的流程。
初步重建: 使用 GSD 重建出一个初步的 3D GS 物体
x₀。渲染与抛光: 将
x₀渲染成图像ŷ₀。这张图可能带有瑕疵。然后,将ŷ₀输入到一个预训练好的 2D 图像到图像的扩散模型(一个“图像美化”模型)中,生成一张更干净、更逼真的“抛光后”的图像y_aux。复用与再引导: 接下来是关键一步。将这张抛光后的高清图像
y_aux作为新的、更优质的引导目标,再运行一次或几次 GSD 的视图引导采样过程。迭代优化: 这个“3D重建 → 2D渲染 → 2D抛光 → 3D再引导”的过程可以迭代进行数次。每一次迭代,2D 模型都能提供一个更逼真的渲染目标,从而帮助 3D 模型优化 GS 的几何和纹理细节,反过来,更优的 3D 模型又能渲染出更好的初始图像送给 2D 模型。
这个迭代过程形成了一个强大的正反馈循环,最终可以同时提升三维模型的几何精度和渲染视图的真实感。
总结
总的来说,GSD 论文的贡献可以归纳为以下几点:
新颖的表示与模型组合: 首次将强大的扩散生成模型直接应用于原始的高斯溅射表示,为单视图三维重建问题提供了一个全新的、高效的解决方案。
高效灵活的视图引导机制: 提出了一种在推理阶段通过可微分渲染进行梯度引导的策略。这种方法非常灵活,因为它解耦了生成先验的学习和视图条件的施加,并且理论上可以轻松扩展到多视图重建。
创新的迭代优化流程: 设计了一个 3D 和 2D 扩散模型协同工作的“抛光与复用”机制,有效地解决了 GS 渲染中可能出现的瑕疵问题,显著提升了最终的视觉质量。
通过这些技术创新,GSD 在标准的 CO3D 数据集上取得了超越当时最先进方法的性能,无论是在渲染图像的质量指标(PSNR, LPIPS)上,还是在三维几何的准确性指标(F-score, Chamfer Distance)上,都展现出了强大的竞争力。
DiffGS: Functional Gaussian Splatting Diffusion (NeurIPS 2024)
输入 (Input):
对于无条件生成:一个随机噪声向量。
对于条件生成:
一段文本描述 (Text Prompt)。
一张2D图像 (Single Image)。
一个不完整的3DGS模型 (Partial 3DGS)。
一个3D点云 (Point Cloud)。
输出 (Output):
一个全新的、完整的、高质量的3D高斯溅射 (3DGS) 模型,可用于实时渲染。
解决的任务 (Task):
从零开始生成3D高斯溅射模型。3DGS因其离散和非结构化的特性,很难直接用标准的生成模型(如扩散模型)来创建。
DiffGS通过一个核心创新解决了这个问题:它不直接生成离散的高斯点,而是先学习生成三个连续的 “高斯函数”(分别代表几何、颜色和变换)。然后,通过一个专门设计的提取算法,将生成的连续函数“离散化”回一个完整的3DGS模型。这套流程巧妙地让强大的扩散模型可以用于高质量3D内容的创作。
概述
这篇论文提出了一种名为DiffGS的新型三维内容生成框架。它的核心目标是解决直接生成3D高斯溅射 (3D Gaussian Splatting, 3DGS) 的难题。传统的3DGS在渲染速度和质量上表现优异,但其本身是一种由大量离散、非结构化的高斯基元组成的表达方式,这使得直接用生成模型(如GAN或扩散模型)来创造新的3DGS非常困难。
DiffGS的核心创新在于,它不直接生成离散的高斯点集,而是提出了一种 “函数式” 的表示方法,将一个离散的3DGS场景巧妙地转化为三个连续的函数。然后,它利用一个变分自编码器 (VAE) 和一个潜在扩散模型 (Latent Diffusion Model, LDM) 来学习并生成这三个函数。最后,通过一个专门设计的高斯提取算法,将生成的连续函数重新离散化,得到最终的3DGS物体。
这种方法巧妙地绕开了处理离散、非结构化数据的难题,使得强大的深度生成模型可以被应用于高质量、高效率的3DGS内容创作中。
Motivation
这篇论文的动机主要源于现有3D内容生成技术的瓶颈:
传统方法的局限性:过去的3D生成模型大多基于神经辐射场 (NeRF)。虽然NeRF能生成高质量视图,但其体积渲染过程计算成本高昂,导致渲染速度缓慢,难以满足实时交互应用的需求。
3DGS的优势与挑战:近年来,3D高斯溅射 (3DGS) 作为一种新的3D表示方法,通过使用数以万计的3D高斯基元来表达场景,实现了前所未有的实时渲染速度和高保真度,被认为是下一代3D表示的有力竞争者。然而,这种优势也带来了新的挑战:
离散性与非结构性:一个3DGS场景本质上是一个无序的、数量可变的“高斯点云”。每个高斯基元都包含位置、形状(旋转、缩放)、颜色和不透明度等属性。这种离散和非结构化的特性,使得在图像、视频等结构化数据上被验证有效的生成模型(如卷积网络、Transformer)无法直接应用。
现有3DGS生成方法的不足:为了解决生成难题,一些同期的工作尝试将高斯基元“装入”一个结构化的体素网格 (Voxel Grid) 中,然后利用成熟的体素生成模型来间接生成高斯。但这种方法有几个明显的缺点:
计算成本高:高分辨率的体素网格会带来巨大的计算和内存开销。
数量受限:生成的高斯数量受到体素分辨率的限制,难以生成非常精细的物体。
信息损失:体素化过程本身可能会引入信息损失,影响最终生成的高斯质量。
DiffGS的出发点:正是为了克服以上所有挑战,作者提出了一个全新的思路——我们能否不依赖体素,而是找到一种方法,将离散的3DGS表示为一个连续的、适合神经网络处理的形式? 这就是“函数式表示”的由来,也是本文最核心的动机和贡献。
Architecture
DiffGS的整体架构可以理解为一个分为训练和生成两个阶段的系统。
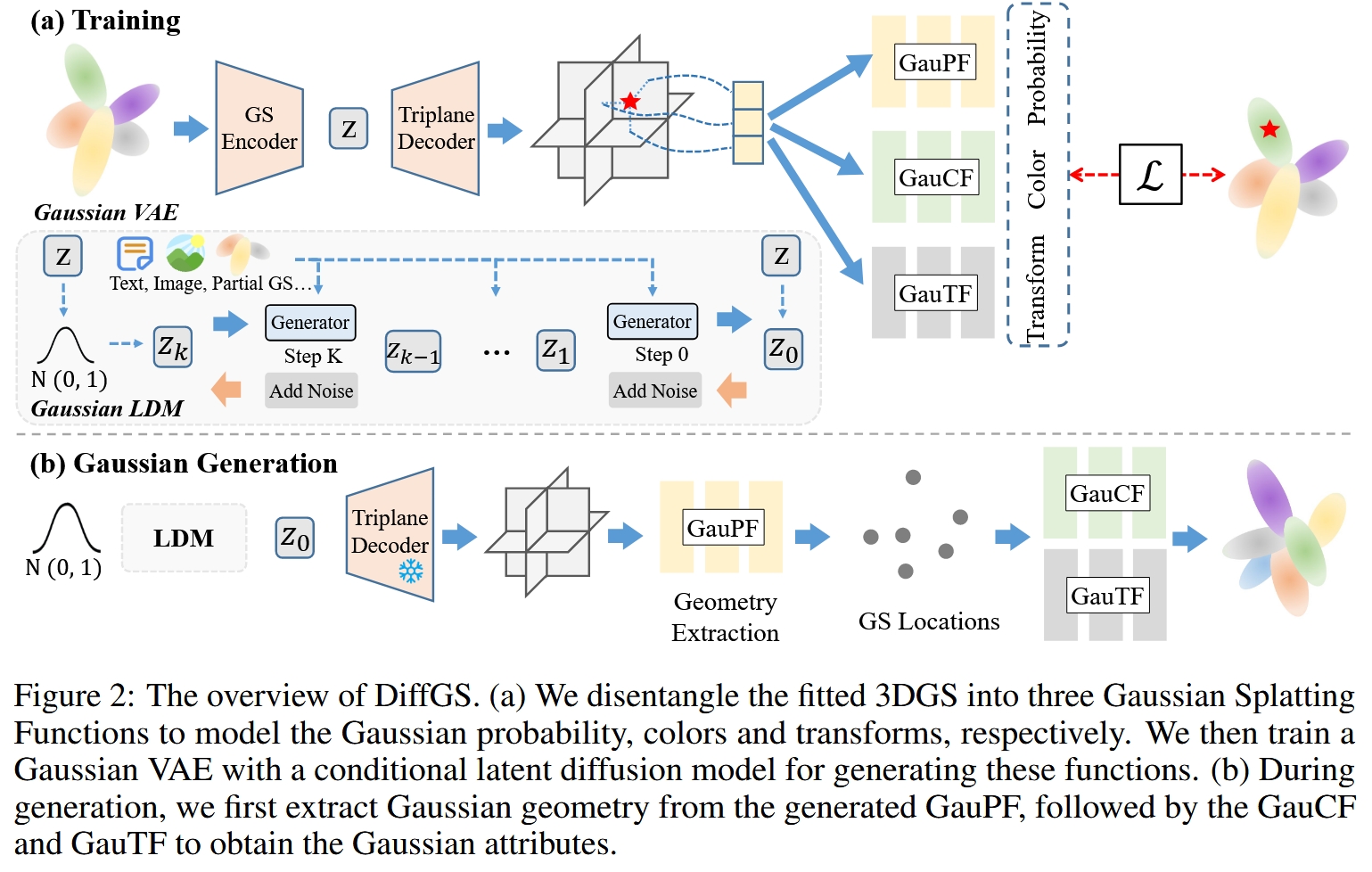
训练阶段: 此阶段的目标是学习如何将一个3DGS场景压缩成一个紧凑的潜在向量 (latent vector),并能从这个向量中恢复出场景。这通过一个高斯变分自编码器 (Gaussian VAE) 来实现。
输入:一个已经拟合好的3DGS场景(包含N个高斯基元)。
函数式解耦:首先,这个离散的3DGS被转换为我们后面会详细介绍的三个连续函数:高斯概率函数 (GauPF)、高斯颜色函数 (GauCF) 和 高斯变换函数 (GauTF)。
高斯VAE (Gaussian VAE):
编码器 (GS Encoder):将输入的3DGS场景编码成一个低维的潜在向量
z。解码器 (Triplane Decoder):将潜在向量
z解码成一个三平面 (Triplane) 特征表示。这是一个高效的3D特征场。函数预测器 (Predictors):三个小型的神经网络(MLP)从三平面特征场中采样,并分别预测出上述三个函数的值。
潜在扩散模型 (Latent Diffusion Model, LDM):在训练好VAE之后,所有训练数据的3DGS都被编码成潜在向量
z。然后,一个标准的LDM在这个潜在空间z上进行训练,学习如何从一个纯高斯噪声逐步去噪,最终生成一个有效的潜在向量z。
生成阶段 (Inference): 当需要创造一个全新的3D物体时,流程如下:
生成潜在向量:训练好的LDM从一个随机噪声开始,生成一个新的潜在向量
z_new。如果需要条件生成(例如根据文本生成),则在去噪过程中会引入文本条件的引导。解码为函数:将
z_new输入到VAE的解码器中,得到该新物体的三个连续函数(GauPF, GauCF, GauTF)的表示(通过三平面和预测器)。高斯提取:使用论文提出的高斯提取算法,从表示几何的GauPF中采样并优化得到高斯基元的位置。
属性查询:将得到的位置坐标输入到GauCF和GauTF中,查询得到每个高斯基元的颜色、旋转、缩放和不透明度。
输出:最终得到一个全新的、完整的、可用于实时渲染的3DGS场景。

图1:DiffGS的整体流程图,清晰地展示了训练(上)和生成(下)两个阶段。
Method
1. 3D高斯溅射简介
一个标准的3DGS场景由N个高斯基元 G = {g_i} 组成。第 i 个高斯基元 g_i 的几何由其中心位置 μ_i 和一个3D协方差矩阵 Σ_i 定义。为了便于优化,协方差矩阵 Σ_i 通常被分解为一个旋转四元数 r_i 和一个三维缩放向量 s_i。此外,每个高斯还有外观属性,即颜色 c_i 和不透明度 α_i。
所以,每个高斯基元可以由一组参数 {μ_i, r_i, s_i, c_i, α_i} 来完整定义。
2. 核心思想:函数式高斯溅射表示 (Functional Gaussian Splatting Representation)
这是DiffGS的基石。作者将一个离散的3DGS场景 G 解耦并表示为三个连续函数:
高斯概率函数 (Gaussian Probability Function, GauPF)
目的:这个函数用于表示物体的几何形状。
定义:对于3D空间中的任意一个查询点
q,GauPF(q)的输出是一个在[0, 1]之间的概率值,表示这个点q是一个高斯基元中心的概率有多大。真值构建:在训练时,如何定义这个概率的“真值”呢?作者提出了一个巧妙的方法:对于一个查询点
q,它真实的概率值取决于它与场景中所有真实高斯中心{μ_i}的最近距离。具体来说,其概率真值定义为:其中
min ||q - μ_i||计算了点q到所有高斯中心的最短距离。λ是一个截断函数,用于过滤掉过大的距离。τ是一个连续函数(例如exp(-x)或线性映射),它将这个距离映射到[0, 1]的概率区间。直观上,一个点离真实的高斯中心越近,它成为高斯中心的概率就越高。作用:通过学习这个函数,模型就隐式地学会了整个物体的几何表面在哪里。
高斯颜色函数 (Gaussian Color Function, GauCF) & 高斯变换函数 (Gaussian Transform Function, GauTF)
目的:这两个函数用于表示物体的外观和属性。
定义:与GauPF不同,这两个函数的输入不是空间中的任意点,而是已知的高斯中心位置
μ_i。GauCF(μ_i)预测该位置高斯基元的颜色c_i。GauTF(μ_i)预测该位置高斯基元的旋转r_i、缩放s_i和不透明度α_i。
设计原因:作者认为,只有在确定了一个点是高斯中心之后,讨论它的颜色、形状等属性才有意义。GauPF负责“找位置”,而GauCF和GauTF负责在找到的位置上“赋属性”。这种设计实现了几何和外观的解耦。
通过这三个函数,一个离散、非结构化的3DGS就被完美地转化为了一个连续、可微分的函数表示,为神经网络的生成任务铺平了道路。
3. 高斯变分自编码器与潜在扩散模型 (Gaussian VAE and LDM)
高斯VAE (Gaussian VAE):
编码器:输入一个3DGS场景,输出一个潜在向量
z。解码器:将
z解码为一个三平面特征场t。对于任何一个3D查询点q,可以通过在这三个正交平面 (xy,xz,yz)上进行三线性插值来获得其特征向量f_q。函数预测器:三个独立的MLP网络
ψ_pf,ψ_cf,ψ_tf,它们将从三平面中查询到的特征f_q作为输入,分别预测出该点的概率、颜色和变换属性。训练目标:VAE的训练损失函数包含两部分:
重建损失:预测出的函数值与真值之间的L1损失,确保VAE能够准确地恢复出原始的3DGS函数表示。
KL散度损失:一个正则化项,强制编码器产生的潜在空间
z的后验分布Q(z|G)接近一个标准正态分布P(z) = N(0, I)。这使得潜在空间变得平滑、连续,便于后续的扩散模型在上面进行学习和采样。
潜在扩散模型 (LDM):
该模型在VAE学习到的潜在空间
z上进行训练。它学习的是一个标准的去噪过程:给定一个加了噪声的潜在向量
z_t和时间步t,模型需要预测出所添加的噪声ε。条件生成:为了实现可控生成(如text-to-3D),可以将文本、图像等条件的嵌入向量通过交叉注意力 (Cross-Attention) 机制注入到扩散模型的U-Net结构中,从而引导生成过程。

4. 高斯提取算法 (Gaussian Extraction Algorithm)
这是从生成的连续函数回到离散3DGS的最后一步,也是至关重要的一步。
Octree引导的几何采样 (Octree-Guided Geometry Sampling):
目标:从生成的GauPF中找到概率最高的N个点,作为高斯基元的中心。
挑战:如果对整个3D空间进行密集采样,计算量将是巨大的。
解决方案:使用八叉树 (Octree) 进行高效的渐进式采样。
从一个包裹整个空间的立方体开始(八叉树的根节点)。
评估这个立方体内部的平均高斯概率。如果概率很高,就将其细分为8个更小的子立方体。
重复这个过程
L层。这样,采样过程会自动聚焦到物体表面等高概率区域,而忽略掉空旷的低概率区域。在最深层的、被保留下来的小立方体中,均匀地采样出
N个初始的“代理点 (proxy points)”。这些点是对真实高斯中心的粗略估计。
使用GauPF优化几何 (Optimizing Geometry with GauPF):
代理点的位置还不够精确。为了进一步提纯,作者将这些代理点的坐标
{p_i}视为可学习的参数。然后通过梯度上升来优化这些点的坐标,优化的目标是最大化它们在GauPF函数上的输出值。其优化目标(损失函数)可以写为:
通过最小化这个负的概率和,代理点会被“推”向GauPF的概率峰值处,从而得到更精确的高斯中心位置
μ̂_i。
提取高斯属性 (Extracting Gaussian Attributes):
一旦确定了所有高斯基元的最终中心位置
μ̂_i,最后一步就很简单了。将这些位置坐标
μ̂_i依次输入到已经生成的GauCF和GauTF函数中(通过查询三平面特征并送入预测器),直接计算出每个高斯对应的颜色c_i、旋转r_i、缩放s_i和不透明度α_i。
至此,一个完整的、包含 N 个高斯基元的新3DGS场景 G_new 就被完全生成了。
总结
DiffGS是一篇在3D生成领域具有高度创新性的工作。它通过以下几个关键步骤,成功地将强大的扩散模型应用于具有挑战性的3DGS生成任务:
动机清晰:准确地指出了直接生成3DGS的困难所在,并针对现有方法的不足提出了改进方向。
核心创新:提出了将离散3DGS函数化的巧妙思想,通过GauPF, GauCF, GauTF三个函数将非结构化数据转化为连续表示,是整个模型的基石。
架构优雅:采用了成熟的VAE+LDM架构,在学习压缩表示的同时,利用LDM强大的生成能力在规整的潜在空间中进行创作。
技术闭环:设计了高效的八叉树引导的提取和优化算法,成功地将生成的连续函数还原为高质量的离散高斯基元,完成了从生成到可渲染的完整闭环。
该方法不仅在无条件生成任务上取得了优于以往方法的效果,还展示了在文本、图像、部分3DGS补全等多种条件生成任务上的强大潜力,为未来的实时、高质量3D内容创作提供了一个非常有前景的新方向。
Last updated
Was this helpful?